Senaste nytt › Forums › Kitesurfing › Konfen Kitesurfing › Hur bra kryssar en kite?
-
johnk;505782 wrote:För att svara på frågan:
Genomsnittligt VMG för kite = 0. När man kryssat lite så hoppar man downwind och hamnar där man började. Vi kommer aldrig till någon kryssningsboj.Aloha…
Vi är ju för fan kitare och inga teknologer som åker runt på vattnet och analyserar.
Hur påverkas förövrigt medelvinden på Ölands nordkust om man
vinklar foten 22 grader bakåt istället för 20 när man kantar, temperaturen på vattnet är 14.7 grader celsius, brädans kantradie är 7,2 meter och stropparna är svarta? :confused2: -
skiter man i…… ut å ha kul på vattnet istället för att tänka så mycket
-
@Gadget 505958 wrote:
Aloha…
Vi är ju för fan kitare och inga teknologer som åker runt på vattnet och analyserar.
Hur påverkas förövrigt medelvinden på Ölands nordkust om man
vinklar foten 22 grader bakåt istället för 20 när man kantar, temperaturen på vattnet är 14.7 grader celsius, brädans kantradie är 7,2 meter och stropparna är svarta? :confused2:Färgen på stropparna påverkar faktiskt inte lika mycket som man tror, det är faktiskt viktigare vilken tid på året det är. Torskens vandring påverkar ytspänningen vilket i sin tur påverkar resultatet.
-
Jag vet att de e fett IG att pissa i motvind iaf… Men det stog inte på min gps så nu smakar man piss i flabben
-
@gh0st 505980 wrote:
Färgen på stropparna påverkar faktiskt inte lika mycket som man tror, det är faktiskt viktigare vilken tid på året det är. Torskens vandring påverkar ytspänningen vilket i sin tur påverkar resultatet.
Afan… e de så alltså. Så min neonrosa kardborband hjällper inte ett skit med andra ord?.
-
Haha.. fan va nördig jag måste vara, tycker detta kan va rätt intressant. 🙂
-
@Krillan82 505984 wrote:
Afan… e de så alltså. Så min neonrosa kardborband hjällper inte ett skit med andra ord?.
tyvärr inte lika mycket som man kan tro.
-
ahh shit, someone better tell sourra his c@ckring was a waste of money…
-
It’s spelled ”klackring” and is common among finlandian gypsys. I haven’t seen it since that time you borrowed it and gave me a ”what ring?”-reply when I asked to get it back. Oh well, I had a feeling it was 10 years out of fashion and it’s made out of fool’s gold so there wasn’t that much of a loss.

-
haha I just had a flashback of you carrying a concealed knife and drinking a bottle of vodka on a stolen bike…
-
Rasmus_W;505663 wrote:Bara nyfiken, vad är ett typiskt VMG (velocity made good) för en typisk kitare? VMG när man kryssar rakt mot vinden är alltså din fart i knop * cosinus för vinkeln du håller mot vinden.
Har för mig en formulavindsurfare gör 7 knop i vmg och monstertrimaraner som kostar miljarder kommer upp mot kanske 10-15 eller så.
Givet konstant vind, ett polardiagram och en önskad kurs, hur ska man segla för att komma fram fortast? Denna eviga fråga tål att funderas på – speciellt för sle kites
Jag började ställa upp problemet och har lite funderingar på hur man ska angripa det. Började med att ställa upp det som ett analytiskt optimeringsproblem med två kurser, sedan med en kontinuerlig viktfunktion (oändligt många kurser). Det blev ganska långa uttryck, så jag angrep istället problemet numeriskt. Med ett ändligt antal kurser (diskretisering av problemet) och villkor som att man inte kan tillbringa negativ tid på en kurs blir problemet direkt ett linjärt program på standardform. Med lite data från Seacart 30 och octave fick jag fram den optimala lösningen. (jag provade först med data från farr 40 one design men det var inte lika intressant, jag är ju trots allt trimaranseglare). Efter att ha experimenterat med lite olika kurser och vindstyrkor känns det som att jag börjat få kläm på problemet:
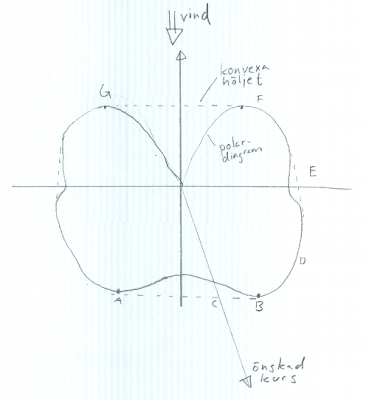
Alla möjliga kombinationer av segling enligt polardiagrammet bildar det
”konvexa höljet” (eng. convex hull) av polardiagrammet. Man kan tänka såhär: man spenderar en viss tid på varje kurs, en faktor som är större än noll. Summan av alla faktorer för alla kurser är ett. Detta är definitionen på en konvex kombination, och följaktligen är konvexa höljet det som går att få ur – det går inte att segla fortare än konvexa höljet!
Med denna insikt så kan problemet med optimal segling reduceras till att man gör såhär:- hitta konvexa höljet för polardiagrammet (trivialt, görs enkelt med penna och linjal, se streckade linjen i figuren)
- för den önskade kursen, sök skärningen med konvexa höljet (punkt C på bilden)
- Optimala kombinationen av kurser är de kurser där konvexa höljet möter polardiagrammet. (punkt A och B på bilden)
Detta kanske låter komplicerat men det är vad seglare vetat länge, när man ska mot vinden måste man kryssa! Det är dock framförallt medvind och vid val mellan olika stora segel (t ex vid punkt E på bilden) man behöver fundera lite mer över detta.
Några mycket intressanta slutsatser kan dras
- det är INTE är vmg mot målet som ska maximeras i varje enskilt tillfälle – det gör alltså inget att vmg är lågt eller negativt sålänge man seglar enligt receptet ovan, man hämtar hem det i genomsnitt. Att få negativt VMG kan hända om skärningsvinkeln är större än 45 grader från/mot vinden, något som ofta händer snabba båtar i svag vind.
- så länge målet ligger i ett område innanför optimala skärningsvinklarna t ex på medvind eller kryss gäller det att alltid skära på de optimala vinklarna. På bilden gäller detta i området F-G (kryss) och A-B (medvind) samt vid E.
För båtar med olika segel, t ex screacher och gennaker kan det vara lönsamt att hålla lite lägre kurs med ett större segel och sedan hämta hem höjden med mindre segel. Detta ges av om polardiagrammet är konvext (polardiagrammet sammanfaller med konvexa höljet) för den önskade kursen!
-
kvabbso;506091 wrote:Givet konstant vind, ett polardiagram och en önskad kurs, hur ska man segla för att komma fram fortast? Denna eviga fråga tål att funderas på – speciellt för sle kites
Jag började ställa upp problemet och har lite funderingar på hur man ska angripa det. Började med att ställa upp det som ett analytiskt optimeringsproblem med två kurser, sedan med en kontinuerlig viktfunktion (oändligt många kurser). Det blev ganska långa uttryck, så jag angrep istället problemet numeriskt. Med ett ändligt antal kurser (diskretisering av problemet) och villkor som att man inte kan tillbringa negativ tid på en kurs blir problemet direkt ett linjärt program på standardform. Med lite data från Seacart 30 och octave fick jag fram den optimala lösningen. (jag provade först med data från farr 40 one design men det var inte lika intressant, jag är ju trots allt trimaranseglare). Efter att ha experimenterat med lite olika kurser och vindstyrkor känns det som att jag börjat få kläm på problemet:

Alla möjliga kombinationer av segling enligt polardiagrammet bildar det
”konvexa höljet” (eng. convex hull) av polardiagrammet. Man kan tänka såhär: man spenderar en viss tid på varje kurs, en faktor som är större än noll. Summan av alla faktorer för alla kurser är ett. Detta är definitionen på en konvex kombination, och följaktligen är konvexa höljet det som går att få ur – det går inte att segla fortare än konvexa höljet!
Med denna insikt så kan problemet med optimal segling reduceras till att man gör såhär:- hitta konvexa höljet för polardiagrammet (trivialt, görs enkelt med penna och linjal, se streckade linjen i figuren)
- för den önskade kursen, sök skärningen med konvexa höljet (punkt C på bilden)
- Optimala kombinationen av kurser är de kurser där konvexa höljet möter polardiagrammet. (punkt A och B på bilden)
Detta kanske låter komplicerat men det är vad seglare vetat länge, när man ska mot vinden måste man kryssa! Det är dock framförallt medvind och vid val mellan olika stora segel (t ex vid punkt E på bilden) man behöver fundera lite mer över detta.
Några mycket intressanta slutsatser kan dras
- det är INTE är vmg mot målet som ska maximeras i varje enskilt tillfälle – det gör alltså inget att vmg är lågt eller negativt sålänge man seglar enligt receptet ovan, man hämtar hem det i genomsnitt. Att få negativt VMG kan hända om skärningsvinkeln är större än 45 grader från/mot vinden, något som ofta händer snabba båtar i svag vind.
- så länge målet ligger i ett område innanför optimala skärningsvinklarna t ex på medvind eller kryss gäller det att alltid skära på de optimala vinklarna. På bilden gäller detta i området F-G (kryss) och A-B (medvind) samt vid E.
För båtar med olika segel, t ex screacher och gennaker kan det vara lönsamt att hålla lite lägre kurs med ett större segel och sedan hämta hem höjden med mindre segel. Detta ges av om polardiagrammet är konvext (polardiagrammet sammanfaller med konvexa höljet) för den önskade kursen!
Jag har blivit upplyst
Logga in för att svara.
